LC 1504: Intuition | Ref. to Maximal Rectangle in a Histogram.

Find the problem description here. If you would like to read the solution in leetcode platform, find it here.

Intuition

First Part:

I solved it first using $O(m * n * n)$ where m is the number of rows in the matrix and n is the number of columns in the matrix.

Let me explain how. Let us categorize the rectangles into three types:

Horizontal rectangles with height 1 and width >= 2.
Vertical rectangles with width 1 and height >= 2.
Every other rectangle.

If you can observe carefully, using the 1 and 2 information computed from points, we can know the number of rectangles of type 3 originated from a certain point at the current instance.

Consider we are computing the number of rectangles from last (bottom-up approach).

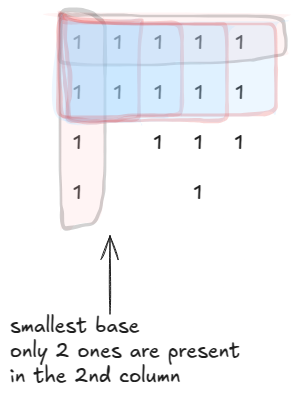
Here, you can see all the possible rectangles (roughly) that have top-right one as their top-right one.

In the image, I have marked both the vertical and horizontal rectangles (pinkish background). The count of those can be immediately gathered by using the number of vertical rectangles formed using the below one, and the number of horizontal rectangles formed using the right one.

The remaining rectangles, when we go from the left to the right column-wise, they depend on the lowest number of ones present vertically. As you can see, there will be a 2x2 formed with the 2nd column. And that column having the minimum ones which is 2 determines the number of rectangles that we can get later.

So, for every cell, we can maintain two states, which is the number of horizontal rectangles it can gather and the number of vertical rectangles it can gather (1xn and mx1).

To get the count of other rectangles, we have to iterate either column-wise or row-wise and determine the count. Simple. Hope you understood this approach.

But, this approach will take $O(m * n * n)$ .

Second Part:

(The reason I came up this approach is because yesterday (i.e., August 20, 2025) cause of the daily problem, I went ahead and solved the Maximal Rectangle in a Histogram and the Maximal Rectangle in a Matirx problems)

By looking at the matrices, you can realize that row by row (or column by column, it is the way you think) you can compute the number of rectangles. It is just the way we found out the Maximal Rectangle present in a matrix. Or the Maximal Rectangle present in a Histogram.

The concept is simple:

Take a histogram like below. You can see that I have drawn the rectangles that can be spread out on either side maintaining the same height as any given bar in the histogram.

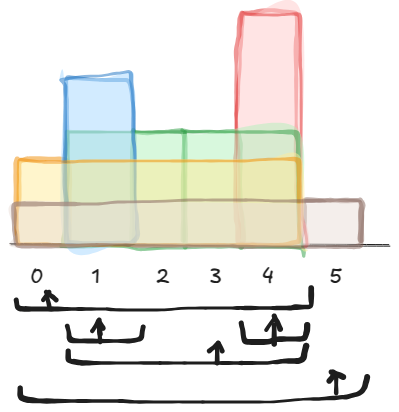
So, the bar at 0 can spread till 4 maintaining it's same height. The bar at 1 only can spread itself. Bars at 2 and 3 are of same length, they can spread till 1 to the left and 4 to the right. Same goes with the others.

As you can observe, each bar can spread till the previous smaller and the next smaller (exclusive).

Hence, if we can find those, we can find the maximum rectangle.

In the similar manner, for the current problem, we can get total number of rectangles as well. So, the height remains the same and we will have our choices for the left & the right boundaries, till the minimum from either sides.

Hope you understood the solution.

The approach uses a single monotonic stack which maintains the elements in strictly increasing order. Whenever, the current element is lesser than the top of the stack that means, the top of the stack has found the previous smaller and the next smaller. We can just count the number of rectangles using that.

Complexity

Time complexity: $O(m*n)$

Code

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int count = 0;
        int m = mat.size(), n = mat[0].size();
        // this stores number of ones from the base
        // if they exists consecutively
        vector<int> heights(n, 0);

        for (const auto& row : mat) {
            // compute the ones from the current base/row
            // just imagine a floating histogram
            for (int j = 0; j < n; ++j) {
                // if zero, reset the count
                if (row[j] == 0)    heights[j] = 0;
                // if not, increment the base count
                else                heights[j]++;
            }

            stack<int> st;
            st.push(0); // maintain indices

            for (int i = 1; i <= n; ++i) {
                // if the current height is lesser than the top of the stack
                while (!st.empty() && (i == n || heights[st.top()] >= heights[i])) {
                    // top of the stack becomes the element in focus
                    int current = st.top(); st.pop();
                    int height = heights[current];
                    // current height is the next smaller for above
                    // previous is the previous in the stack or none
                    // as we maintain the stack in strictly increasing order
                    int previous = -1, next = i;
                    if (!st.empty())    previous = st.top();
                    
                    // number of rectangles newly formed from the base
                    // when height of the base spreads either side
                    // this includes the intermediates formed from height
                    // but not from the width
// height * number of choices for the left boundary * number of choices for the right boundary
                    count += (height * (current - previous) * (next - current));

                }

                st.push(i);
            }
        }

        return count;
    }
};

Cheers! Good luck!