Find the problem description here. If you would like to read the solution in leetcode platform, find it here.

if you haven't solved the first part of this problem yet, please do. the brute-force solution is pretty straight-forward. let me explain:

the points need to form a pair such that the first point is at the upper left corner and the second point is at the lower right corner. kind of like forming a pretty rectangle. another given condition is, you shouldn't have any other point present on this formed rectangle anywhere. even on the edges. simplifying this, if you assume the two points are $(x_1, y_1)$ at the upper left corner and $(x_2, y_2)$ at the lower right corner then, the conditions look something like this:

$x_1 \leq x_2$
$y_1 \geq y_2$
$\forall (x_i, y_i), \space i \neq 1,2:\quad \neg \big( x_1 \leq x_i \leq x_2 \space \wedge \space y_2 \leq y_i \leq y_1 \big).$

hope you understand the above conditions. you can simply replicate this onto a three part loop and solve it in $O(n^3)$ time complexity.

but, this works only for the first part of the problem. in the second part of the problem, which is the problem at hand, the constraints have increased from having n value as 50 to having n value as 1000. so, previously 50 * 50 * 50 fit under $10^8$ . but, $1000 * 1000 * 1000 = 10^9$ is greater than $10^8$ . so, the $O(n^3)$ solution will give you TLE.

let us optimize this.
let us take an example: [(1, 4), (5, 2), (2, 5), (4, 1), (3, 3)]

now, let us sort them simply based on the x-coordinate in non-decreasing order. why you may ask? if we sort them w. r. t. x-coordinate, for every pair of points at the indices i and j where i < j, the first condition we discussed automatically becomes true. hence, we have eliminated that check.

following this, let us add one more sorting layer here, which is 'if x coorindates are equal then, sort them based on the y-coordinate in non-increasing order`. if you think about it, for any two coordinates with x-coordinate equal, this 2nd sorting layer will possibly make the second condition also true.

the array now becomes this: [(1, 4), (2, 5), (3, 3), (4, 1), (5, 2)] we have settled down on the sorting that we have to do. now, we need to pair every point to the point that appears before it in the order. because those are the pairs that have chances to be valid as we have sorted the points based on their x-coorindates.

but, somehow we need to know whether there are any points that appear on the rectangle formed by a pair and also present in between them.

have a look at this illustration:

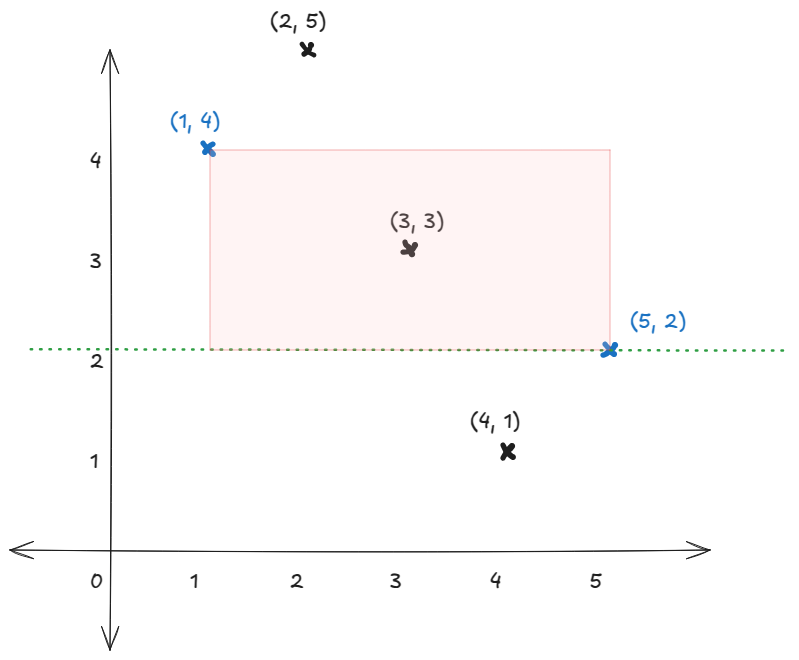
consider the pair (1, 4) and (5, 2). while iterating, we just have to maintain the minimum y-coordinate that we have that is greater than the y-coordinate of the point present at the lower right corner i.e., points that appear above or on the green line. because, the points like (4, 1) with y-coordinate lesser, anyway won't make it to the rectangle.

now, to form a pair:

the y-coordinate of the point at hand which is the point that is expected to be at upper left corner need to be greater than or equal to the y-coordinate of the point that we are handling which is the point at lower right corner.
the minimum y-coordinate appeared till that point (considering all the points that are in between the point at hand and the point we are handling according to x-axis) need to be greater than or equal to the y-coordinate of the point at hand (i.e., point at upper left corner).

from here, everything else is pretty self-explanatory. look at the code to understand even better.

Time complexity: $O(n^2)$

Code

class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        int n = points.size();
        int count = 0;

        sort(points.begin(), points.end(), [](vector<int>& a, vector<int>& b) {
            if (a[0] == b[0]) {
                // sort by y axis in descending order
                return a[1] >= b[1];
            }

            return a[0] <= b[0];
        });

        // for every lower right corner
        for (int i = n - 1; i >= 0; i--) {
            // point we are handling (lower right corner)
            int x1 = points[i][0];
            int y1 = points[i][1];

            // minimum y-coordinate greater than or equal to y1 in-between
            int middleY = INT_MAX;

            // select a valid upper left corner
            for (int j = i - 1; j >= 0; j--) {
                // point at hand
                int x1 = points[j][0];
                int y2 = points[j][1];

                if (y2 >= y1 && middleY > y2) {
                    count++;
                    middleY = min(middleY, y2);
                }
            }
        }

        return count;
    }
};

good luck!

LC 3027: Explained | With Illustration.

Code