LC 898: Standard solution but explained.

Find the problem description here. If you would like to read the solution in leetcode platform, find it here.

---

Intuition

1. Think about all the sub-arrays that are ending at a certain index j.
2. For all these sub-arrays, if you observe carefully, adding one by one to the current number from the current index i.e., if the current index is j then, we add the number at j first, and then the numbers at j - 1, j - 2, so on till 0, it will always increase the OR value.
3. The increase in the OR value can be seen as an increase in the number of set bits. And in the running iteration, there won't be any decrease at all. It is always monotonically increasing the OR value from the current index till 0.
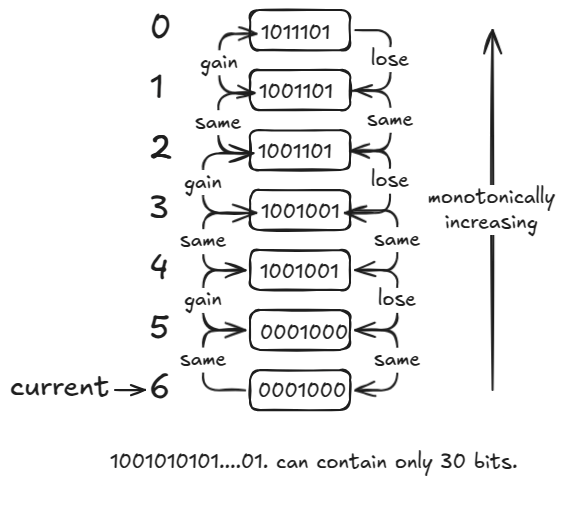
4. Hence, by storing the previous OR values from the sub-arrays that are ending at the previous index j - 1, we can easily obtain all the unique OR values from the sub-arrays ending at the current index j. Refer to the image below for better understanding.

The monotonic nature of this tells you that any current set will contain atmost 30 unique numbers, because there can be only 30 bits to set as per the given constraints. All the explanation above is to prove the point that the time complexity will be $O(30*n)$ and not $O(n^m)$ where m is the number of unique sub-array OR values obtained.

---

Approach

We can utilize two sets, one for maintaining the previous OR values obtained from the sub-arrays ending j - 1 and another for getting the OR values obtained from the sub-arrays ending at the current index j. Also, result set to maintain all the unique OR values.

---

Complexity

• Time complexity: $O(30*n)$

---

Code

class Solution {
public:
    int subarrayBitwiseORs(vector<int>& arr) {
        unordered_set<int> st;
        unordered_set<int> pre, curr;

        for (int i = 0; i < arr.size(); ++i) {
            for (auto it : pre) {
                st.insert(it | arr[i]);
                curr.insert(it | arr[i]);
            }

            st.insert(arr[i]);
            curr.insert(arr[i]);

            pre = curr;
            curr.clear();
        }

        return st.size();
    }
};

good luck!